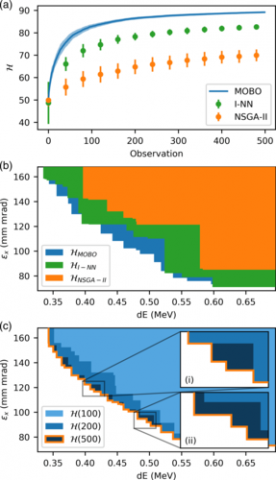
Multiobjective Bayesian optimization for online accelerator tuning
Currently online tuning of accelerator parameters to improve performance is limited to solving single objective problems, ie. minimizing the beam brightness or bunch length from a photoinjector. These objectives often are in competition with one another, where minimizing one objective comes at a deleterious cost to another. We wish to experimentally identify the ideal trade-off between competing objectives when it is expensive or time-consuming to perform an objective measurement, known as solving the multi-objective optimization problem. Previously, this has only been possible in simulated environments. However, our paper describes an algorithm that can determine this trade-off between objectives in an experimentally efficient manner.
This work contributes towards the goals of Theme 3: Beam Dynamics and Control which aims to develop novel methods for improving control of high brightness accelerators. Using these advanced control methods, CBB enables improved transport of beams once they are generated to free electron laser and collider applications.This advancement solves an extremely common experimental or computational problem faced by those in the accelerator, physical, chemical and biological scientific fields. As such, it is applicable towards solving any multi-objective experimental problem where it is difficult or expensive to make an objective measurement.
Scientists in the physics community will, for the first time, be able to characterize the ideal experimental trade-off between competing objectives in order to improve and have greater control over their experiments that require optimization.
Reference:
R. Roussel, A. Hanuka, and A. Edelen, “Multiobjective Bayesian optimization for online accelerator tuning,” Phys. Rev. Accel. Beams, vol. 24, no. 6, p. 062801, Jun. 2021, doi: 10.1103/PhysRevAccelBeams.24.062801. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevAccelBeams.24.062801