Functional Form of the Superconducting Critical Temperature from Machine Learning
S. R. Xie, G. R. Stewart, J. J. Hamlin, P. J. Hirschfeld, and R. G. Hennig
A graph with Tc from experiment (K) on the x-axis. On the y-axis is TC predicted (K). The scatter graph shows that Allen-Dynes RMSE = 0.30 K and Sisso Eq. (4) RMSE=0.25 K follow predictions closely, while Mod. McMillan RMSE = 0.92 K strays slightly further from predicted.
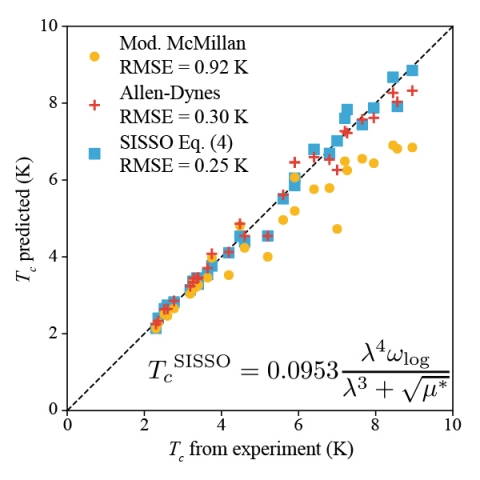
Predicting the critical temperature Tc of superconductors is a notoriously difficult task. Here we show that machine learning can deduce a practical equation for Tc and identify the relevant physical parameters. We demonstrate that incorporating physical knowledge into equation-based machine learning has the potential to learn physical relations on relatively small data sets and expect this new paradigm to generate a significant number of follow-on efforts not just to superconductivity, but to a variety of other materials design problems.This machine-learning approach provides the opportunity to identify relevant measures of electronic structure crucial for superconductivity that can enable a high-throughput search for novel superconductors with higher critical temperature and fields for application in accelerator cavities.